| Heart of Avalonia |
Note-13 Basal Shear stress
Basal shear stress is the component of stress directed parallel to the ground at the base of an ice sheet or glacier. Globally, basal shear stress results from the gravitational force pulling a mass of ice down hill. Locally, basal shear stress reflects a combination of gravitational force and the force exerted on a specific region of ice by adjacent ice.
The usual reason for analyzing basal shear stress is to understand the flow of glacial ice and to link rates of glacial ice flow to topographic conditions and the state (temperature, water content) of ice comprising a glacier. Basal shear stress is strongly controlled by the rheology of ice. Ice is a highly deformable medium at deviatoric stress levels exceeding 0.1 MPa and will normally yield so as to relieve excessive amounts of shear stress. Although ice is a shear-thinning non-Newtonian viscous fluid, when ice is under sufficient hydrostatic pressure to prevent cavitation, the laws of fluid dynamics dictate that local deviatoric stress can substantially exceed 0.1 MPa in areas where concentrated flow leads to an elevated rate of ice deformation.
In this Technical Note 13, basal shear stress will be discussed with regard to three special conditions. First, the substrate underlying deforming glacial ice will be assumed to be non-granular, that is, bedrock. Second, the ice will be considered to be cold throughout and thus not subject to basal sliding. Third, ice thickness will be assumed to exceed 100 m, providing an energy barrier to ice fracturing or cavitation. These conditions appear reasonable in the context of observations of bedrock disruption by ice in areas of the Avalon Peninsula that have been affected by subglacial bedrock frost heave.
Although glacial ice flow is the usual concern when considering basal shear stress, the focus of observations in the present paleoglaciological context lies entirely on relict bedrock disruption. Glacial artifacts such as striations, plucking, streamlined erosion patterns or the placement of till are attributed to the movement of glacial ice. A cold-based glacier does not slide and moves only by internal deformation. However, cold-based glacial ice that is frozen to bedrock and not in a state of perfect mechanical equilibrium (that is, a condition of zero creep) will load bedrock in shear. The continuous shear stress applied to bedrock by ice that is stationary relative to bedrock at the ice-bedrock boundary can, in principle, modify bedrock characteristics and leave a record. Specifically, the process of bedrock erosion by subglacial ice extrusion is subject to modification by shear stress acting on the bedrock being eroded.
Detailed calculation of basal shear stress patterns beneath a cold glacier is complex. The complexity follows from the variable rheology of ice and the irregularities in the surface of the substrate. It is reasonable to argue that shear loading of bedrock by cold glacial ice is a process demonstrating extreme sensitivity to initial conditions and that the outcome is nonlinear and chaotic. A preserved record of the impact of shear loading, with local resolution down to centimeter scales, will be hard to interpret, but will place boundaries on generalizations regarding the evolution of cold glaciers anchored to bedrock.
The usual reason for analyzing basal shear stress is to understand the flow of glacial ice and to link rates of glacial ice flow to topographic conditions and the state (temperature, water content) of ice comprising a glacier. Basal shear stress is strongly controlled by the rheology of ice. Ice is a highly deformable medium at deviatoric stress levels exceeding 0.1 MPa and will normally yield so as to relieve excessive amounts of shear stress. Although ice is a shear-thinning non-Newtonian viscous fluid, when ice is under sufficient hydrostatic pressure to prevent cavitation, the laws of fluid dynamics dictate that local deviatoric stress can substantially exceed 0.1 MPa in areas where concentrated flow leads to an elevated rate of ice deformation.
In this Technical Note 13, basal shear stress will be discussed with regard to three special conditions. First, the substrate underlying deforming glacial ice will be assumed to be non-granular, that is, bedrock. Second, the ice will be considered to be cold throughout and thus not subject to basal sliding. Third, ice thickness will be assumed to exceed 100 m, providing an energy barrier to ice fracturing or cavitation. These conditions appear reasonable in the context of observations of bedrock disruption by ice in areas of the Avalon Peninsula that have been affected by subglacial bedrock frost heave.
Although glacial ice flow is the usual concern when considering basal shear stress, the focus of observations in the present paleoglaciological context lies entirely on relict bedrock disruption. Glacial artifacts such as striations, plucking, streamlined erosion patterns or the placement of till are attributed to the movement of glacial ice. A cold-based glacier does not slide and moves only by internal deformation. However, cold-based glacial ice that is frozen to bedrock and not in a state of perfect mechanical equilibrium (that is, a condition of zero creep) will load bedrock in shear. The continuous shear stress applied to bedrock by ice that is stationary relative to bedrock at the ice-bedrock boundary can, in principle, modify bedrock characteristics and leave a record. Specifically, the process of bedrock erosion by subglacial ice extrusion is subject to modification by shear stress acting on the bedrock being eroded.
Detailed calculation of basal shear stress patterns beneath a cold glacier is complex. The complexity follows from the variable rheology of ice and the irregularities in the surface of the substrate. It is reasonable to argue that shear loading of bedrock by cold glacial ice is a process demonstrating extreme sensitivity to initial conditions and that the outcome is nonlinear and chaotic. A preserved record of the impact of shear loading, with local resolution down to centimeter scales, will be hard to interpret, but will place boundaries on generalizations regarding the evolution of cold glaciers anchored to bedrock.
Basics
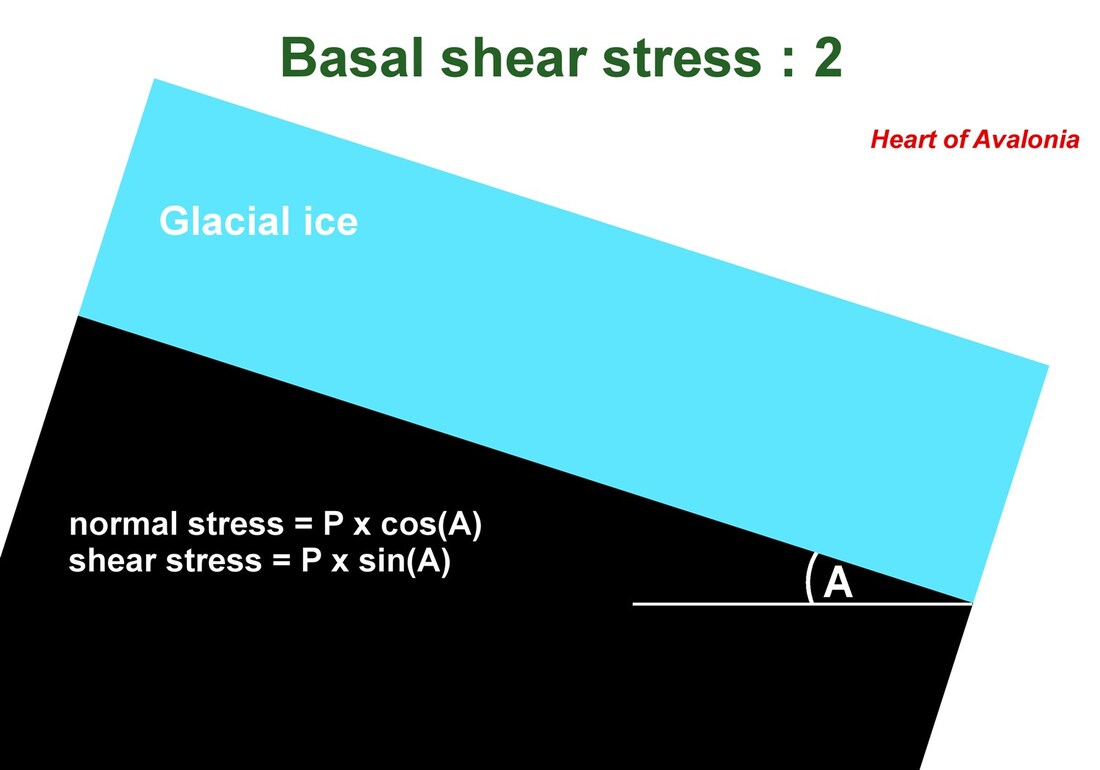
The above diagram shows a condition of mechanical equilibrium where glacial ice has no tendency to deform in creep and the shear stress at the ice-bedrock interface is zero. The normal stress, P, is the hydrostatic pressure at the base of the glacier, generated by the weight of the overlying ice.
An ice sheet of uniform thickness, lying on a flat, sloping bedrock surface is shown above. The basal shear stress in this geometry is easy to calculate, but the geometry is not likely representative of conditions on the Avalon Peninsula during deglaciation. The Avalon has been heavily eroded by multiple episodes of deep glaciation and is relatively flat when averaged over kilometer-scale distances. If the bays surrounding the Avalon deglaciated rapidly because of rising sea levels at the end of the Pleistocene, then thick ice sheets remaining over land areas would slope steeply toward the coast. The slope of the ice sheets would potentially exceed the slope of the underlying bedrock by a large angle.
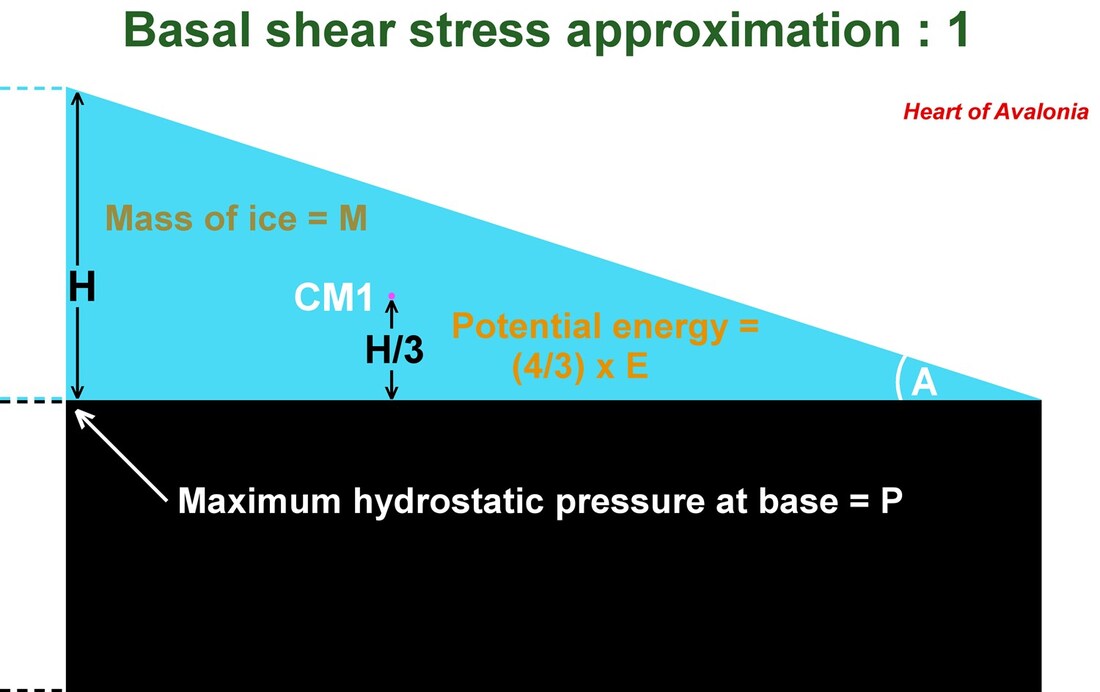
The above diagram shows a simplified model for potential conditions existing on the Avalon Peninsula during the Younger Dryas cold period. The bedrock topography is essentially flat and horizontal, while the overlying cold ice sheet slopes toward the coast at angle, A. The maximum hydrostatic pressure, P occurs inland where the ice levels off to its maximum thickness, H. The potential energy of the ice is given in terms of a reference potential energy, E, defined in diagram 2 below.
If ice were a rigid medium (creep rate = zero at all shear stress levels), then there would be no basal shear stress in the geometry shown above. If ice were a low-viscosity Newtonian fluid (like water), then little shear stress would be applied to the base as the sloping configuration quickly collapsed. Because ice possesses an intermediate rheology, the above geometry allows for a significant shear loading of the base while the system gradually deforms toward mechanical equilibrium.
Without knowing the details of ice temperature, slope, flow history, and the effects of these parameters on ice rheology, the basal shear stress corresponding to the highly simplified model shown above can only be approximated. One way to obtain an approximation is to consider the change in potential energy of a mass of ice deforming from the above-illustrated shape to the equilibrium shape under the influence of gravity. Total stress is determined by the loss in potential energy accompanying the descent of a unit volume of ice.
If ice were a rigid medium (creep rate = zero at all shear stress levels), then there would be no basal shear stress in the geometry shown above. If ice were a low-viscosity Newtonian fluid (like water), then little shear stress would be applied to the base as the sloping configuration quickly collapsed. Because ice possesses an intermediate rheology, the above geometry allows for a significant shear loading of the base while the system gradually deforms toward mechanical equilibrium.
Without knowing the details of ice temperature, slope, flow history, and the effects of these parameters on ice rheology, the basal shear stress corresponding to the highly simplified model shown above can only be approximated. One way to obtain an approximation is to consider the change in potential energy of a mass of ice deforming from the above-illustrated shape to the equilibrium shape under the influence of gravity. Total stress is determined by the loss in potential energy accompanying the descent of a unit volume of ice.
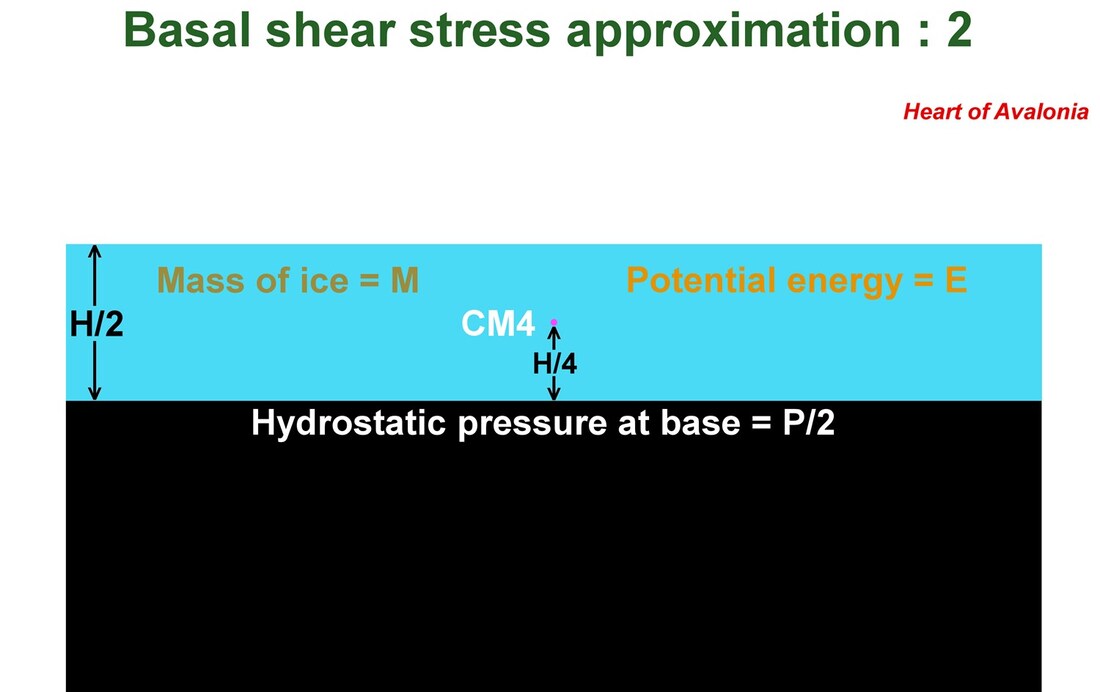
The above diagram 2 shows the same volume of ice as in the preceding diagram 1, but configured in a state of mechanical equilibrium. This configuration represents the end state after all creep ceases in the sloping configuration shown in diagram 1. A zero of potential energy can be defined by the potential energy of the block of ice resting with its center of mass, CM4, level with the ground. The potential energy of the block as diagrammed above then corresponds to the energy needed to raise the block by a distance H/4. This potential energy corresponds to a total stress at the base of P/2. All of the stress is normal stress.
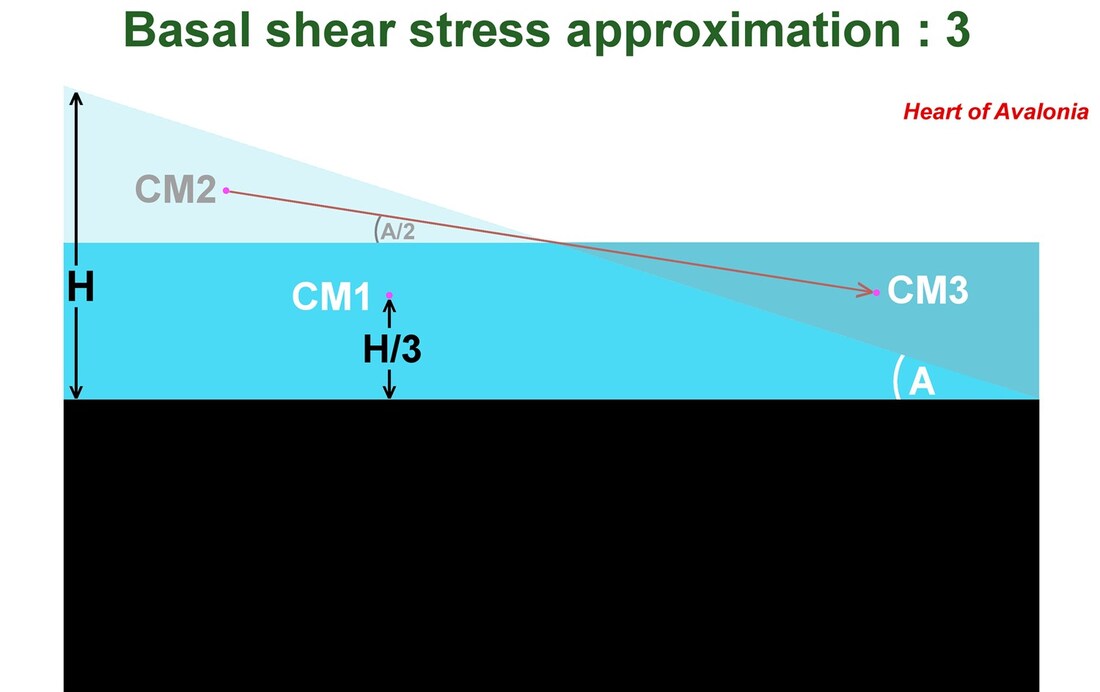
The above diagram 3 shows the transfer of mass needed to convert the sloping-ice configuration of diagram 1 into the equilibrium configuration of diagram 2. The ice cross-section shown in diagram 1 is a right triangle with center of mass (centroid, CM1) located at a height of H/3 as shown above. A similar triangle comprising 1/4 of the mass of the full ice sheet, with a center of mass CM2 can be rotated 180 degrees about CM2 (energy neutral operation) and then translated down a line sloping at angle A/2 to rest with the center of mass (formerly CM2) at the new position, CM3. The location, CM3, is lower than the location of CM2 by H/3. The change in potential energy associated with the repositioning of 1/4 of the ice mass to a location lowered by H/3 is 1/3 of the of the total potential energy, E, of the ice block as defined in diagram 2.
The total stress associated with lowering the gravitational potential energy, E, of the ice mass, M, by sliding the mass down an inclined plane sloping at an angle, A/2, can be resolved into normal and shear components as illustrated in diagram 4 above. The above diagram 4 overstates the total stress (hence its components) by a factor of 3 since the energy change achieved via ice deformation as illustrated in diagram 3 is E/3.
The above diagram 5 summarizes the results of the energy/stress analysis presented in diagrams 1 through 4 above. For example, if an ice sheet slopes at a uniform 20 degrees while resting on flat substrate, the basal shear stress imparted to the bedrock is approximately 2.6% of the hydrostatic pressure beneath the thickest portion of the ice sheet.
Stress concentration
Concentration of basal shear stress is related to elevated rates of ice deformation near the glacier base. Because ice is shear thinning (viscosity declines roughly with the cube of increasing shear stress), large increases in ice creep rate are associated with small increases in shear stress. This type of non-Newtonian rheology limits the ability of glacial ice to load bedrock in shear. Nevertheless, concentration of basal shear stress, even if only by a few percent or tens of percent, is potentially significant in generating observable indications of bedrock shear-loading by glacial ice. As shear stress changes, bedrock response can change, with the effects of changes in shear loading being more easily recognized than the effects of uniform shear loading.
Two special cases of basal shear stress concentration are significant because the cases occur commonly and the topographic circumstances leading to enhanced shear loading are easy to identify. Case 1: Ice is forced against an obstruction. Case 2: Ice accelerates as it moves into a less confined area. These cases are illustrated in the following diagrams.
Two special cases of basal shear stress concentration are significant because the cases occur commonly and the topographic circumstances leading to enhanced shear loading are easy to identify. Case 1: Ice is forced against an obstruction. Case 2: Ice accelerates as it moves into a less confined area. These cases are illustrated in the following diagrams.
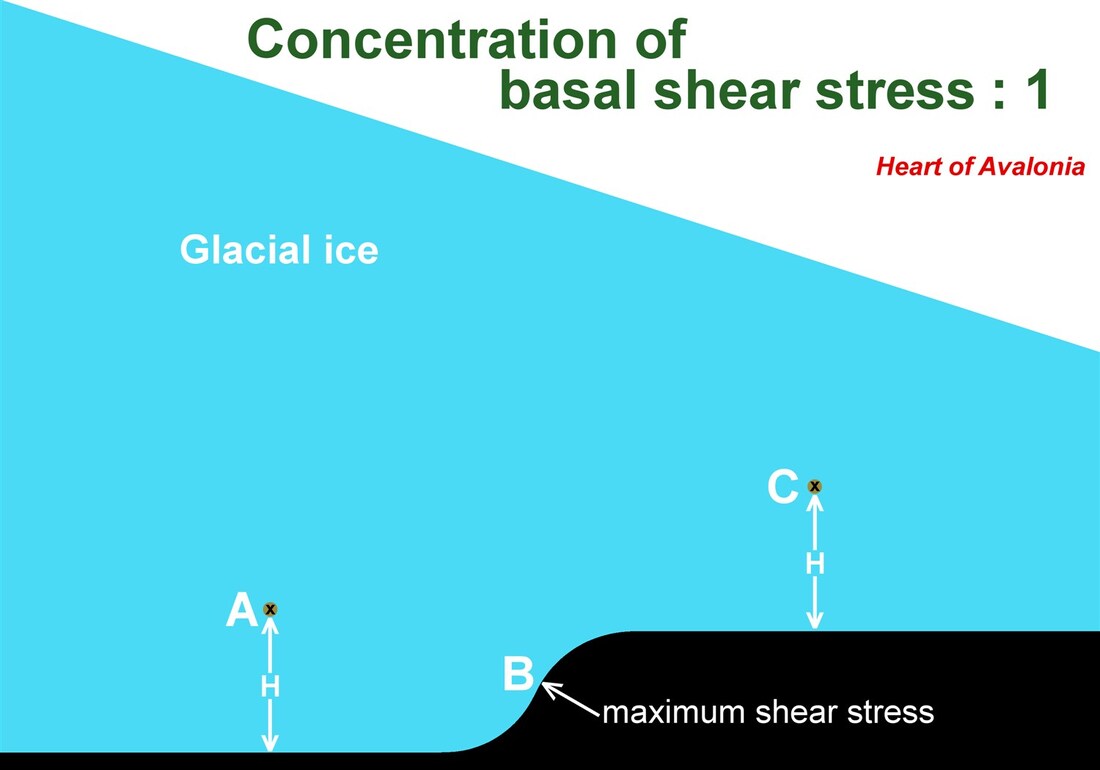
The above diagram 1 shows a low obstruction hindering the flow of glacial ice deforming in creep. The glacier is not drawn in vertical scale to match the obstruction, but rather the glacier is assumed to be at least an order of magnitude thicker than the obstruction is high. In this instance, ice creep velocity at point "A" closely matches ice creep velocity at point "C", since both points are at equal height above the ground and the obstruction is assumed not to significantly concentrate or impede the average glacial ice flow. At points near "B", ice must accelerate because ice has further to travel in order to clear the obstruction. The theoretical ratio of the ice velocity at mid-slope to the incoming or outgoing horizontal ice velocity rises with the reciprocal of the cosine of the slope angle, reaching infinity for a vertical slope. In reality, slow-moving or stationary near-ground ice in the vicinity of "B" prevents the realized ice path from approaching a vertical angle. Shear thinning in this geometry is not strongly effective in mitigating the shear stress imparted to the bedrock at "B". As ice viscosity diminishes, ice velocity increases at points close to the ground near "B".
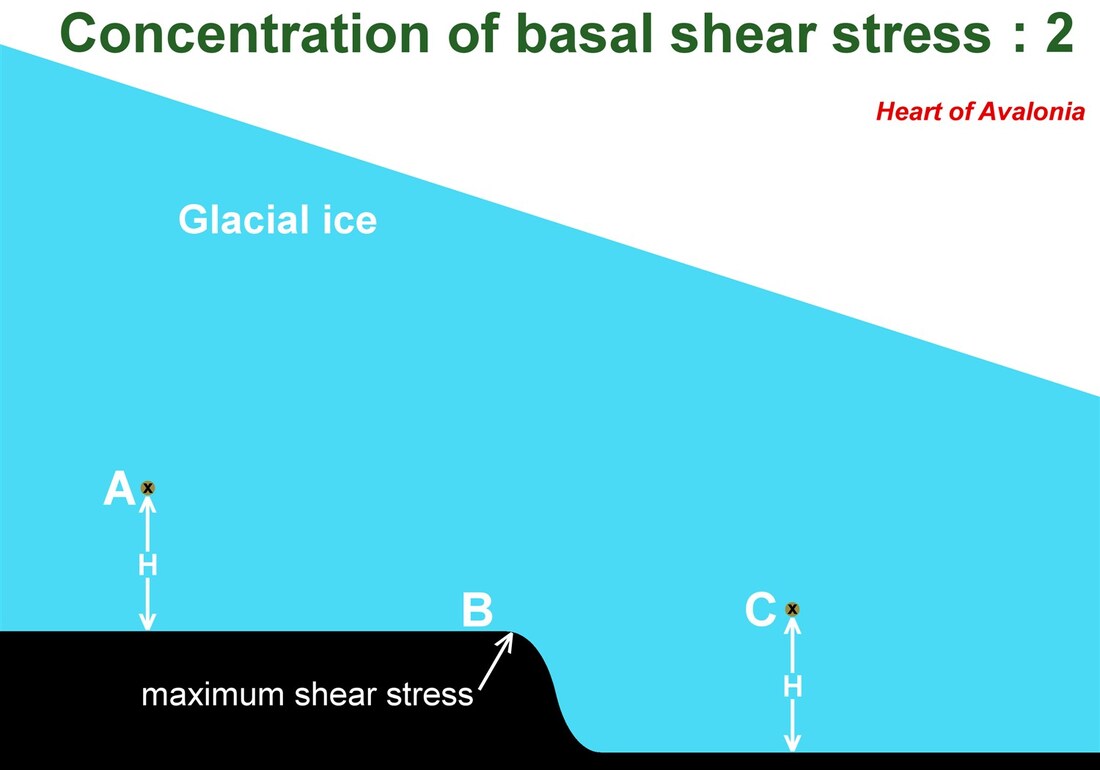
As with the previous diagram 1, the above diagram illustrates a relatively low topographic feature beneath a thick glacier. The velocity of ice at point "A" matches the velocity of ice at point "C". The velocity of ice at ground level at point "B" is zero, but immediately to the right of "B", ice velocity increases toward the value to be reached at "C". The increase in horizontal ice velocity at "B" requires an infill of ice from above so as to conserve ice volume (ice is assumed incompressible and not subject to cavitation). The near-ground ice velocity at points above "B" is increased by the descending ice needed to augment the horizontal flow. Thus the shear stress at "B" is higher than at points immediately to the left of "B". To the right of "B", points near the ground on the downward-sloping surface experience a reduced total stress because tensile stress associated with the friction of ice deformation partially counteracts the hydrostatic pressure of the overlying glacial ice.
Enhanced shear stress at a lee edge, as illustrated in diagram 2 above, is likely to be particularly effective in generating disruptive effects in bedrock that is asymmetrically confined and weakly confined. The key difficulty in interpreting the effects of shear stress at a lee edge lies in separating the subtle direct effects of shear loading from the more pronounced effects of mechanical displacement of rock by moving ice.
Enhanced shear stress at a lee edge, as illustrated in diagram 2 above, is likely to be particularly effective in generating disruptive effects in bedrock that is asymmetrically confined and weakly confined. The key difficulty in interpreting the effects of shear stress at a lee edge lies in separating the subtle direct effects of shear loading from the more pronounced effects of mechanical displacement of rock by moving ice.
Observations
The observable effects of subglacial shear stress on bedrock are vulnerable to confusion with the effects of ice movement. For example, if a frost-heaved joint block were observed to be tilted relative to the angle of dip of foliation in bedrock substrate, an ambiguity arises. Was the joint block displaced at an angle reflecting a condition of shear stress in the host bedrock, or, was the joint block rotated by the mechanical effect of ice moving in creep just above the ground? In the case of a tilted joint block, the distinction is not greatly significant since ice creep occurring near the ground is related to basal shear stress by an "if and only if" relationship.
Bedrock erosion by subglacial ice extrusion is a process that operates primarily below ground level and, correspondingly, would potentially be influenced solely by shear stress without taking near-ground ice deformation into account. The interest in identifying possible instances of below-ground effects stemming directly from basal shear stress lies in extending the analysis of cold-glacier ice movement into the below-ground environment. Usually, the movement of a glacier over hard bedrock is analyzed in terms of ice and rock comprising separate mechanical systems. If stress in glacial ice can be shown to modify the behavior of below-ground water and ice, and this below-ground water and ice, in turn, modifies the behavior of the overlying glacier, then the overall system becomes intrinsically interconnected. Such an ice-rock system might, in principle, show special characteristics not expected when treating a glacier and its hard bedrock substrate as separate entities. An abundance of subglacial bedrock frost heave occurrences and closely related occurrences of bedrock erosion by ice extrusion, readily observed over large areas of the Avalon Peninsula, suggests the adoption of an ice-rock-system approach whereby a cold glacier is not assumed to "end" at the ice-bedrock interface.
Bedrock erosion by subglacial ice extrusion is a process that operates primarily below ground level and, correspondingly, would potentially be influenced solely by shear stress without taking near-ground ice deformation into account. The interest in identifying possible instances of below-ground effects stemming directly from basal shear stress lies in extending the analysis of cold-glacier ice movement into the below-ground environment. Usually, the movement of a glacier over hard bedrock is analyzed in terms of ice and rock comprising separate mechanical systems. If stress in glacial ice can be shown to modify the behavior of below-ground water and ice, and this below-ground water and ice, in turn, modifies the behavior of the overlying glacier, then the overall system becomes intrinsically interconnected. Such an ice-rock system might, in principle, show special characteristics not expected when treating a glacier and its hard bedrock substrate as separate entities. An abundance of subglacial bedrock frost heave occurrences and closely related occurrences of bedrock erosion by ice extrusion, readily observed over large areas of the Avalon Peninsula, suggests the adoption of an ice-rock-system approach whereby a cold glacier is not assumed to "end" at the ice-bedrock interface.
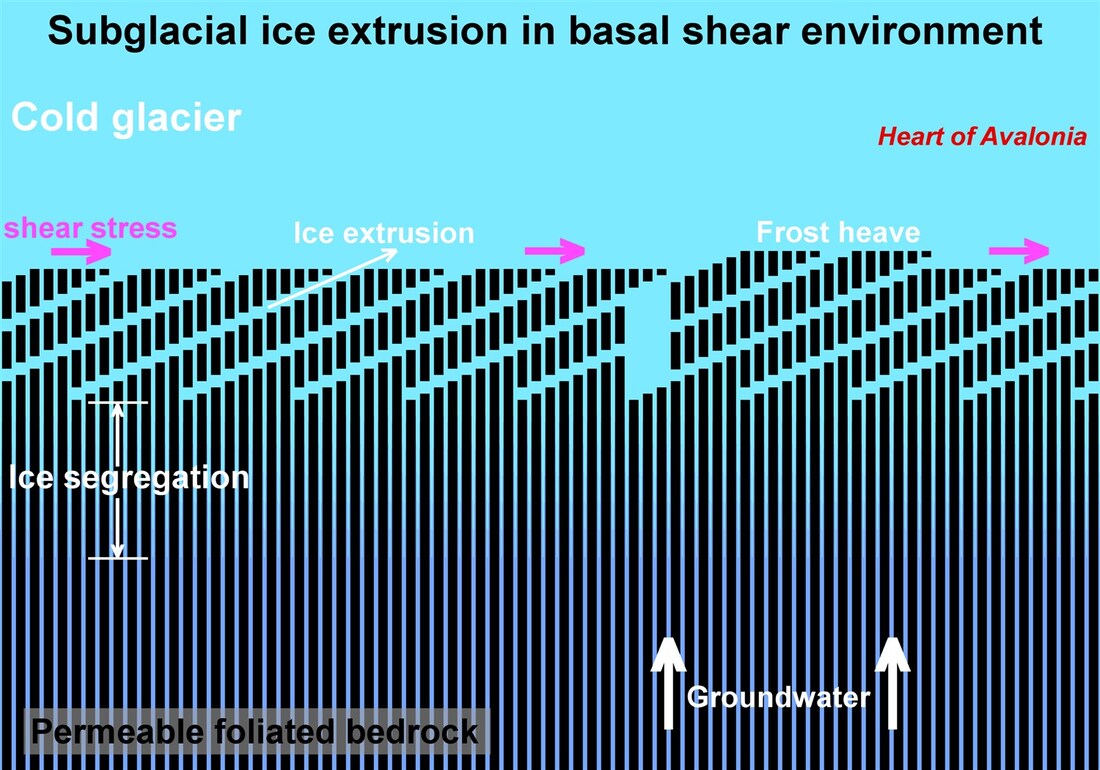
The above diagram shows a possible effect of basal shear stress on bedrock erosion by subglacial ice extrusion. In the absence of basal shear stress, ice extrusion erodes bedrock along channels or grooves that align with tectonically-induced foliation in regionally-metamorphosed bedrock. The erosion by ice extrusion delaminates the bedrock, often yielding a distinctive exaggerated layered appearance, frequently accompanied by abundant bedrock frost heave. The above diagram illustrates bedrock delamination that does not follow foliation, but rather is deflected by an angle related to the presence of basal shear stress at the time that subglacial ice extrusion was occurring. Instead of failing along a continuous plane aligned with the plane of foliation, flattened and aligned grains of rock are cleaved off in a step-wise manner generating a deflected plane of rock delamination. This phenomenon has been observed in the field and two specific details of the observations link the phenomenon to basal shear stress. Firstly, deflection of the plane of delamination is directed top-toward-the-coast, matching the anticipated direction of shear loading by glacial ice. Second, the phenomenon is most pronounced at points of anticipated shear stress concentration, that is, on obstructing slopes and lee edges. The section "Bedrock erosion by subglacial ice extrusion - Part 03" (pending) will present observations supporting the above model.
Return to list of technical notes
Return to list of technical notes
heartofavalonia.org Exploring Geologic History